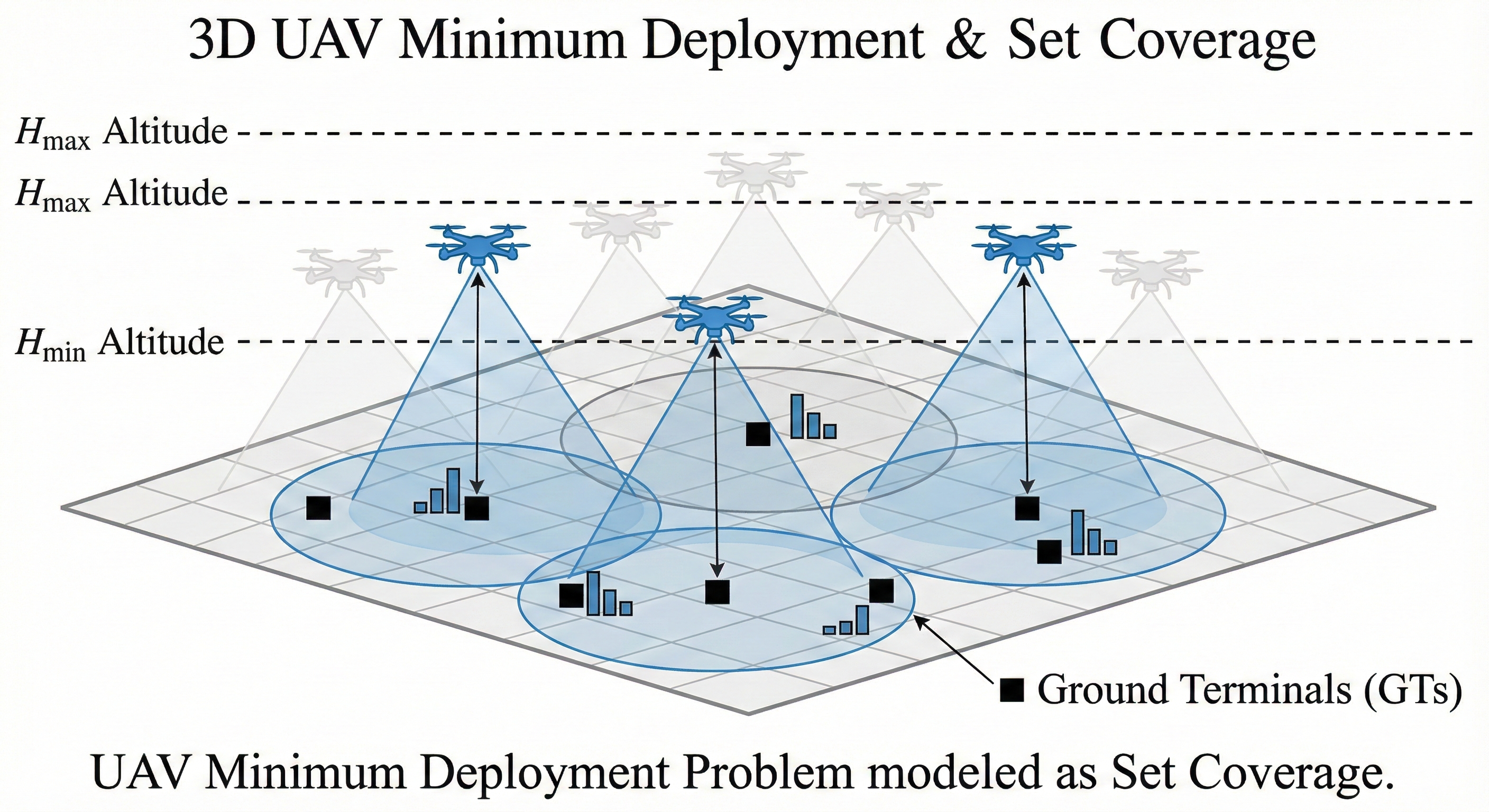
无人机最小部署问题:在三维空间中存在若干固定位置且接入需求已知的地面终端,这些终端只能通过部署在空中的中继无人机接入网络。 每架中继无人机具有受限的留空高度范围(高度上下限)、覆盖半径或链路容量等通信性能约束。 我们的目标是在满足所有地面终端接入需求的前提下,确定所需部署的中继无人机数量最少。这个问题可以建模为集合覆盖问题。
将中继无人机最小部署问题形式化为如下模型:
终端集合: 地面终端集合 U={t1,t2,…,tn},其中 ti 表示第 i 个地面终端。
候选无人机部署方案: 候选部署位置集合 P={p1,p2,…,pm}。 对于每一个候选方案 pj(包含位置、高度等),其能覆盖的地面终端子集为 Sj⊆U。
集合族: 所有候选方案对应的覆盖子集构成集合族 S={S1,S2,…,Sm}。
目标: 从 S 中选出最少的子集,使其并集覆盖 U。
注
Q: 怎么确定UAV的初始的候选位置集合P?可否通过终端集合的位置通过一些特定的模型继而生成一些较为合理的初始位置?
Q: 对于某一具体的UAV,怎么确定其覆盖终端子集Sj?
| 符号 | 定义 |
|---|
| U={1,2,…,n} | 地面终端集合,第 i 个终端位置 (xi,yi) |
| P={p1,…,pm} | 候选 UAV 位置集合,每个候选 pj=(xj,yj,hj) |
| xj∈{0,1} | 决策变量:是否在候选点 pj 部署 UAV |
| yij∈{0,1} | 决策变量:终端 i 是否被无人机 j 服务(即终端 i 在可被无人机覆盖的情况下是否选择无人机 j 为他服务) |
| Pt,fc,B,N0 | 发射功率、载波频率、带宽、噪声功率谱密度 |
| hmin,hmax | UAV 高度限制 |
| Cj,Rmin | UAV 容量限制、最小速率需求 |
判断一个 UAV 是否能服务某个用户,需满足几何与通信约束。
计算几何距离与仰角 水平距离 dijh=(xi−xj)2+(yi−yj)2 三维距离 dij=(dijh)2+hj2 仰角 θij=arctan(dijhhj)
估计 LoS(视距)概率 使用 Al-Hourani 模型:
PLoS(θ)=1+aexp(−b(θ−a))1
其中 a,b 为环境参数(如城市环境 a=9.61,b=0.16)。
计算路径损耗 平均路径损耗(dB):
Lij=PLoS(θij)⋅LLoS(dij)+(1−PLoS(θij))⋅LNLoS(dij)
其中 LLoS 和 LNLoS 为自由空间损耗加上附加损耗 η。
计算信噪比与速率 接收功率 Pr,ij=Pt/10Lij/10 信噪比 SNRij=N0BPr,ij 速率 Rij=Blog2(1+SNRij)
判定覆盖 若 Rij≥Rmin 且 hmin≤hj≤hmax,则认为终端 i 可被候选点 pj 覆盖,即 i∈Sj。
由于部署位置是连续的,通常采用离散化方法生成候选集合 P。
- 水平网格化:在目标区域按步长 g(如 50m)划分网格,取网格点作为水平坐标 (x,y)。
- 高度离散化:对每个水平点,取若干离散高度 h∈{h1,h2,…}。
- 生成集合:所有 (x,y,h) 组合构成候选集合 P。
将问题建模为 0-1 整数线性规划问题:
mins.t.j=1∑mxjj:i∈Sj∑yij≥1,∀i∈U(覆盖约束)yij≤xj,∀i,j(关联约束)i:i∈Sj∑diyij≤Cjxj,∀j(容量约束)xj,yij∈{0,1}
| 算法 | 说明 | 适用场景 |
|---|
| 贪心算法 (Greedy) | 每次选择能覆盖最多终端的候选点 | Baseline,速度快,近似解 |
| 整数规划 (ILP) | 使用 Gurobi/CPLEX 求解精确最优解 | 小规模问题 (n,m 较小) |
| 聚类 + 局部优化 | 先 K-means 分簇,再簇内求解 | 大规模问题,实用性强 |
| 元启发式 (GA/PSO) | 遗传算法或粒子群算法搜索 | 复杂非线性约束 (如 SINR) |
- 载波频率: fc=2 GHz
- 光速: c=3×108 m/s
- 系统带宽: B=10 MHz
- 发射功率: Pt=10 dBm
- 噪声谱密度: N0=−174 dBm/Hz
- 终端最小速率需求: Rmin=5 Mbps
- 单个终端容量: di=0.2−5 Mbps的均匀分布
- 单 UAV 容量: Cmax=50 Mbps
提示
- 指挥/控制(C&C)、低速遥测):60–100 kb/s。这是 3GPP 和多篇论文常用的 C&C 门槛。
- 低速数据 / IoT 设备:10–100 kb/s(取决应用)
- 普通网页/消息/轻量应用:100–500 kb/s(0.1–0.5 Mbps)
- 视频通话 / 标清视频流:500 kb/s – 2 Mbps
- 高清视频流 / 高质量多媒体:2–8 Mbps(或更高)
- 大流量回传 / 高速上网:>10 Mbps
- 路径损耗参数: a=9.61, b=0.16
- LoS 附加损耗: ηLoS=1.0 dB
- NLoS 附加损耗: ηNLoS=20.0 dB
- UAV 高度范围: hmin=100 m, hmax=150 m
- 服务区域: 1000×1000 m²
LoS 概率模型
基于 Al-Hourani 模型,仰角 θ 的 LoS 概率为:
PLoS(θ)=1+a⋅exp(−b⋅(θ−a))1
其中仰角 θ=arctan(d2Dh),d2D 为水平距离。
路径损耗模型
自由空间路径损耗 (FSPL):
LFSPL=20log10(d3D)+20log10(fc)+20log10(c4π)
平均路径损耗:
Lavg=PLoS⋅LLoS+(1−PLoS)⋅LNLoS
其中:
LLoS=LFSPL+ηLoS
LNLoS=LFSPL+ηNLoS
速率计算
接收功率:
Pr=10Lavg/10Pt
信噪比:
SNR=N0⋅BPr
香农容量:
R=B⋅log2(1+SNR)
- xj∈{0,1}: 是否在候选点 j 部署 UAV
- yij∈{0,1}: 用户 i 是否连接到 UAV j
minj∈J∑xj
覆盖约束 (每个用户至少连接一个 UAV):
j∈J∑yij≥1,∀i∈I
关联约束 (只有部署的 UAV 才能提供服务):
yij≤xj,∀i∈I,j∈J
容量约束 (每个 UAV 的总服务需求不超过容量):
i∈I∑di⋅yij≤Cmax⋅xj,∀j∈J
覆盖质量约束 (隐含在候选点生成中):
yij=0,if Rij<Rmin
其中:
- I: 用户集合
- J: 候选部署点集合
- di: 用户 i 的需求
- Rij: 候选点 j 对用户 i 的可达速率
- 候选点生成: 在三维网格中生成候选位置
- 覆盖矩阵预计算: 计算 Rij≥Rmin 的覆盖关系
- ILP 模型构建: 建立上述数学模型
- CBC 求解器求解: 使用分支定界法求解
- 结果提取: 获得最优 xj 和 yij
重要
复杂度分析:
- 时间复杂度: O(∣J∣⋅∣I∣⋅poly(n))
- 空间复杂度: O(∣J∣⋅∣I∣)
算法思路:采用聚类 + 局部搜索 + 自适应分裂的三阶段框架:
初始化与 K 值估算
基于容量约束估算 UAV 数量下界:
Kmin=⌈Cmax∑i∈Idi⌉
全局 K-means 聚类
使用标准 K-means 算法将用户划分为 Kmin 个簇:
{Ck}mink=1∑Ki∈Ck∑∣∣pi−ck∣∣2
其中 pi 为用户 i 的位置,ck 为簇 k 的质心。
递归处理每个簇
Step 1: 局部搜索
对每个簇 Ck,以质心 ck 为中心进行三维搜索:
搜索空间:
Sk={[x,y,h]:∣x−ck,x∣≤Δ,∣y−ck,y∣≤Δ,hmin≤h≤hmax}
寻找满足以下条件的 UAV 位置 u∗=[x∗,y∗,h∗]:
Ri,u∗≥Rmin,∀i∈Ck
i∈Ck∑di≤Cmax
Step 2: 自适应分裂
如果局部搜索失败,对簇 Ck 进行 2-means 分裂:
Ck→Ck1∪Ck2
递归处理子簇,直到:
- 子簇可被单架 UAV 覆盖,或子簇只剩单个用户 (直接部署)
重要
复杂度分析
- 时间复杂度: O(K⋅n⋅d⋅I+K⋅S3⋅R)
- K: 初始簇数, n: 用户数, d: 维度, I: K-means 迭代次数
- S: 搜索范围, R: 递归深度
- 空间复杂度: O(n+K⋅S3)
候选点生成
从终端中心位置和其覆盖圆的交点生成候选部署位置。
候选点剪枝
移除被其他候选点包含的子集,以减少问题规模。
UAV 选取
使用整数线性规划(ILP)找出覆盖所有终端所需的最少 UAV 数量。
分配与精细调优(Minimax 优化)
选择候选点后,将每个终端分配给特定的 UAV(通常是最近的选择),然后优化 UAV 的位置以最小化到其分配终端的最大距离。
每个 UAV k 的优化问题:
令 Sk 为分配给 UAV k 的终端集合,我们想要找到最优的三维位置 u=(x,y,z)。
目标: 最小化最大距离 R:
minR
约束条件:
覆盖约束: 到每个分配终端 pi 的距离必须在 R 范围内:
∥u−pi∥≤R,∀i∈Sk
可行性约束: 距离不得超过终端的通信范围 R3d,i:
∥u−pi∥≤R3d,i,∀i∈Sk
高度约束: UAV 必须在允许的高度范围内:
hmin≤z≤hmax
我们使用 CVXPY 来解决这个二阶锥规划(SOCP)问题。
给定一个有限圆集合:
C={C1,C2,…,Cn},
其中每个 Ci 是平面上的一个圆。
定义覆盖数函数:
f(x)={Ci∈C∣x∈Ci}.
对任意圆子集 I⊆C,定义“覆盖组合区域”:
SI={x∈R2∣{Ci∣x∈Ci}=I}.
即:
SI 表示 恰好被集合 I 中的圆覆盖,并且不被其他圆覆盖的区域。
根据覆盖圆的数量,对所有非空 SI 分类:
Sk={I⊆C∣∣I∣=k,SI=∅},k=1,2,…,n.
速率 → 最小 SNR
信道容量(香农公式)为
R=Blog2(1+SNR)
因此最小所需 SNR 为
SNRmin=2Rmin/B−1.
链路预算(线性形式)
接收功率与发射功率及路径损耗关系为
Pr(d)=L(d)Pt.
噪声功率(线性刻度)为
N=N0B.
因此 SNR 为
SNR(d)=NPr(d)=L(d)NPt.
要求
SNR(d)≥SNRmin
等价于
L(d)≤NSNRminPt.
使用自由空间路径损耗(FSPL)
若路径损耗模型为
LFS(d)=(c4πfd)2,
则代入可得到最大允许距离 (d_{\max}):
(c4πfdmax)2=NSNRminPt
解出最大距离
dmax=4πfcN0B(2Rmin/B−1)Pt.